Обоснование уменьшения противопожарного расстояния менее 6 метров (отступление от Приложения А СП 4.13130)

Заказать расчетное обоснование противопожарных расстояний

Статья из научного журнала ФГБУ ВНИИПО МЧС России «Актуальные вопросы пожарной безопасности», №3 (9), 2021.
Авторы: Леончук П.А., Иващук Р.А., Фомин М.В., Рукавишников М.М.

Рассматриваются особенности нормативного регулирования противопожарных расстояний в части расчетного обоснования их величин. Аргументируется необходимость усовершенствования расчетных методов, закрепленных в СП 4.13130.2013. Осуществляется постановка задачи и приводятся пути ее решения для определения допустимости сокращения противопожарного расстояния до менее чем 6 м. Дается краткий обзор возможностей моделирующих программ, сделан вывод о необходимости решения поставленной задачи как с использованием численных методов, так и путем решения дифференциального уравнения теплопроводности. Приведен возможный алгоритм обоснования противопожарного расстояния на основе полученных зависимостей. Названы инструментальные средства, с помощью которых может быть решена задача обоснования противопожарных расстояний.

Введение

Достаточно новым подходом в противопожарном нормировании явилась нормативно закрепленная методика обоснования уменьшения противопожарных расстояний между жилыми и общественными зданиями, появившаяся при внесении изменения № 1 в СП 4.13130.2013 [1], вступившего в силу 14 августа 2020 года. Согласно требованиям п. А.1.1 Приложения А СП 4.13130.2013, методика определения безопасных противопожарных расстояний между зданиями (далее – Методика) предназначена для расчетной оценки возможности сокращения противопожарных расстояний до величины не менее чем 6 м. В ином случае, когда противопожарное расстояние составляет менее 6 м, следует использовать метод полевого моделирования с определением локальных плотностей радиационных тепловых потоков, и учитывать механизмы переноса тепла посредством конвекции и теплопроводности. Перечисленные механизмы актуальны для случая, когда помимо теплового потока от факела пламени конструкция омывается струей горячих газов, образующих конвективную колонку пожара.

Исходя из этого следует учесть такие величины, как: температура среды у стены здания, соседнего с горящим зданием, плотность радиационных тепловых потоков от очага пожара на участке стены соседнего здания, коэффициент теплоотдачи от газовой среды к стене, теплофизические параметры материала стены, что в целом характерно для случая пожара при воздействии его ограждающие конструкции [2].

Но при этом в самой Методике алгоритм обоснования противопожарного расстояния менее 6 м не представлен.

Учитывая большую значимость для проектировщиков вопроса обоснованного сокращения противопожарных расстояний, предлагается алгоритм проведения расчетов, учитывающий требования Методики по обоснованию противопожарных расстояний менее 6 м.

Методика в качестве критерия допустимого противопожарного расстояния предлагает лишь величины падающих тепловых потоков. Эти величины получены в результате исследований при нагревании поверхностей в условиях, когда температура окружающей среды равна или мало отличается от начальной температуры поверхности, и остается неизменной в течение всего периода нагрева [3]. Так, предельные значения в Методике соответствуют времени нагревания некоторых материалов – древесины, стеклопластика и других материалов – в течение 15 мин. Методикой по определению расчетных величин пожарного риска на производственных объектах предлагаются значения предельных тепловых потоков, полученные при бесконечном времени экспозиции.

В интересующем случае нагрев осуществляется от совместного воздействия тепловых потоков – конвективного потока от обтекающего стену потока горячих газов и радиационных от пламени и от того же потока горячих газов. Поэтому применять представленный критерий – предельно допустимый тепловой поток, полученный при испытании в нормальной атмосфере, – без обоснования не вполне корректно.

Представляет интерес найти эквивалентный падающий тепловой поток Fэкв, равный по тепловому воздействию фактическому потоку, включающему в себя лучистую и конвективную составляющие от омывающей конструкцию горячей струи, и сопоставить его с предельно допустимым тепловым потоком для материала стены. Тогда можно будет сделать вывод о допустимости сокращения противопожарного расстояния.

Общие положения

При отсутствии аналитических, эмпирических, полуэмпирических методов расчета пользуются, как правило, полевыми моделями, которые позволяют моделировать различные физические процессы численными методами [3–5]. В целом возможности численного (полевого) моделирования очень широки. Компьютерные программы позволяют воспроизводить физические процессы любого масштаба – от капиллярных явлений до атмосферных.

Рассмотрим кратко возможности полевых моделей в части моделирования процессов, происходящих при пожаре, и получения параметров, которые должны быть учтены при обосновании противопожарного расстояния.

Надо сказать, что существуют специализированные компьютерные кластеры для запуска параллельных вычислений по полевым моделям, но их использование дорого и не всегда оправдано при проектировании достаточно ординарных объектов [6, 7]. Подавляющее большинство расчетов по полевым моделям выполняются пожарными специалистами на настольных компьютерах. Объем памяти и быстродействие здесь ограничивают возможности моделирования расчетными областями, содержащими 2–3 миллиона ячеек вычислительной сетки в лучшем случае.

Для моделирования противопожарных расстояний линейные размеры вычислительного домена должны составлять десятки метров, а размер ячейки вычислительной сетки при этом составит более 0,1 м. При увеличении количества ячеек и уменьшении размера ячейки задача расчета требует увеличения ресурсов, и стоимость ее выполнения может стать несопоставимой с целями проектирования.

Такие размеры ячеек позволяют достаточно достоверно моделировать динамику газовой среды и радиационного переноса тепла, но непригодны для учета теплоотдачи и теплопроводности внутри твердого тела, которым является стена здания, соседнего с горящим зданием.

Толщина пограничного слоя при обтекании стены струей горячего газа измеряется меньшими величинами [8–10], а так называемые пристеночные функции для моделирования пограничного слоя не всегда показывают достоверный результат на больших ячейках.

Крупная сетка не позволяет воспроизвести распределение температуры по толщине нагреваемого материала. При этом прогрев конструкции, особенно ее поверхности, и является тем показателем, по которому можно будет судить о возможности перехода пожара от одного здания к другому. Например, толщина образца, прогреваемого тепловым потоком при испытании, 20 см [3, 11]. По расчетам, приведенным ниже, и по ссылке, где находится программа для расчетов, можно определить, что в случае древесины на расстоянии 1 см от края обогреваемой поверхности температура на порядок меньше, чем на поверхности.

Явления, которые оцениваются как критерии воспламенения и самовоспламенения [3], а именно искры и появление горения при наличии источника зажигания не могут быть смоделированы с использованием средств, которые обычно используются специалистами по пожарной безопасности вследствие необходимости моделирования таких процессов в высочайшем разрешении. Применение полевой модели становится несоразмерным по затратам, и возникает необходимость в инженерных методах расчета, которые могут быть реализованы иными способами помимо полевых моделей.

Поэтому предлагается использовать полевую модель только в качестве одной из составляющих при обосновании сокращения противопожарного расстояния, а именно для определения локальных плотностей радиационных тепловых потоков и температуры горячих газов, обтекающих конструкции соседнего здания. Т. е. тех параметров, которые наиболее часто и достаточно достоверно вычисляются по полевым моделям, например, при расчетах пожарного риска. Вопросы расчета передачи тепла путем конвекции и теплопроводности могут быть решены аналитическим путем.

Оба рассмотренных процесса – прогрев поверхности от источника теплового излучения в нормальных условиях и при обтекании поверхности потоком горячих газов – подчиняются одним и тем же физическим законам и отличаются только направлениями векторов конвективных тепловых потоков [12]. В первом случае конвективная теплоотдача имеет место от нагреваемой поверхности к окружающей среде, во втором – наоборот, от окружающей среды к поверхности. Хотя, как будет показано ниже, направление вектора конвективного теплового потока в обоих случаях может меняться.

Теоретические основы

Необходимая для обоснования противопожарного расстояния менее 6 м величина эквивалентного теплового потока может быть получена на основе уравнения теплопроводности для рассматриваемого случая [13–15].

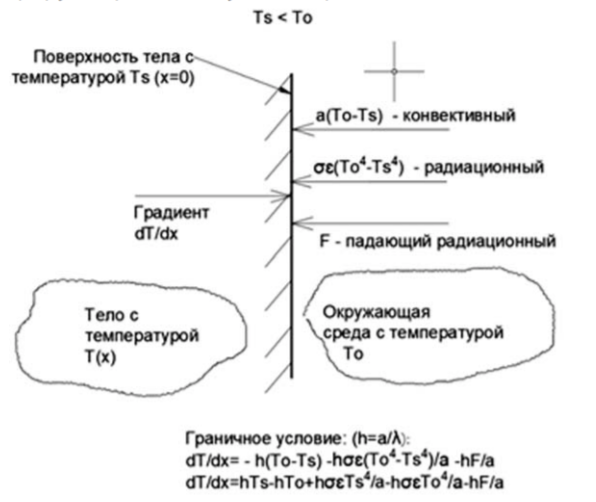
Рассмотрим уравнение теплопроводности для случая, когда на нагреваемую поверхность с ненулевой начальной температурой воздействует падающий тепловой поток от пламени пожара, а также конвективный и лучистый поток от омывающей эту поверхность струи горячих газов [3, 16, 17]. На рис. 1 приведена схема тепловых потоков.

Воспользуемся также некоторыми из методов решения уравнений с помощью изображений функций по Лапласу [13]. Будем рассматривать прогрев полуограниченного твердого тела, когда тепловой поток распространяется вглубь тела в направлении х. Такой подход допустим в течение периода времени, сопоставимого с временем начальной стадии пожара [14]. В нашем случае он составляет около 15 мин, что соизмеримо с временем начальной стадии.

В решении задачи поиска эквивалентного теплового потока используются

следующие физические величины:

T – температура тела, К, являющаяся функцией времени и координаты;

Tн – начальная температура тела, К;

T0 – температура окружающей среды, К;

t – время, с;

a – температуропроводность, м2/с;

ά – коэффициент теплоотдачи, Дж/(м2 · с · К);

λ – теплопроводность, Дж/(м · с · К);

x – расстояние от границы поверхности тела, м;

F – тепловой поток, Дж/(м2 · с);

σ – постоянная 5,67 · 10-8 Вт/ м2 · К4;

ε – приведенная степень черноты системы «окружающая среда – поверхность».

В общем виде уравнение теплопроводности имеет вид:

(1)
Применим к уравнению (1) преобразование Лапласа [13] и запишем его с учетом того, что начальная температура тела равна Tн (2):
Метод оценки воздействия пожара на конструкции здания при обосновании противопожарных расстояний менее 6 метров

(2)
(данное уравнение называется вспомогательным, черточка сверху обозначает изображение функции по Лапласу), где для оптимизации, упрощения и сокращения дальнейших выкладок, как в [13], используется вспомогательная величина:

(3)

Применение метода изображений позволяет уравнение в частных производных (1) привести к дифференциальному уравнению 2-го порядка (2).

Решение уравнения (2) представляет собой сумму общего и частного решений [18]. Общее решение имеет вид:

(4)

Найдем частное решение. Исходя из вида правой части (2), частное решение ищем в виде многочлена нулевой степени B, т. е. числа:

(5)

Для нахождения B подставим это решение в (2). Тогда:

Метод оценки воздействия пожара на конструкции здания при обосновании противопожарных расстояний менее 6 метров

(6), (7)

С учетом (3):

(8)

Решение уравнения (2) имеет вид:

(9)

В рассматриваемом случае используется граничное условие третьего рода [13, 15], при котором также задан тепловой поток на поверхности F. Кроме этого граничные условия запишем с учетом лучистого теплообмена между окружающей средой и стенкой:

(10), (11)

где для оптимизации, упрощения и сокращения дальнейших выкладок, как в [13], используется вспомогательная величина:

(12)

Проиллюстрируем граничное условие рис. 2.

Рис. 2. Построение граничного условия, когда температура среды превышает температуру поверхностиСледует также обратить внимание на то, что в процессе нагревания тела температура поверхности под воздействием теплового потока от пламени пожара может превысить температуру окружающей среды. В этом случае направление конвективного теплового потока меняется, теперь он направлен от стены в окружающую среду. Рассмотрим схему теплообмена в этом случае (рис. 3).

Рис. 3. Построение граничного условия, когда температура среды меньше температуры поверхностиИз рисунка видно, что знаки при величинах, входящих в выражение граничного условия (10), такие же, как и в начале расчета, когда температура среды превышает температуру стены. Таким образом, выражение (10) справедливо и в этом случае. На этом этапе удобно получить искомый эквивалентный тепловой поток.

Вывод расчетных формул

В связи с наличием в уравнении члена в четвертой степени решение такого уравнения чрезвычайно усложняется [13, 19]. Но для целей настоящей статьи (поиска эквивалентного теплового потока) решение такого уравнения и не требуется. Хотя ниже будет представлено решение для более простого случая, когда радиационный тепловой поток от горячих газов учитывается увеличением коэффициента теплоотдачи [13, 14].

Запишем граничное условие (11) в изображениях:

Запишем выражение (15) для начальных условий, соответствующих прогреву конструкции тепловым потоком, когда начальная температура среды равна температуре стены, т. е. искомым эквивалентным тепловым потоком. Начальную температуру среды обозначим Tэкв0. Видно, что слагаемые

равны и сокращаются, поскольку начальная температура среды равна начальной температуре стенки. Тогда:

(16)

Согласно теореме существования и единственности решения дифференциального уравнения второго порядка [18], для того, чтобы искомый эквивалентный тепловой поток прогревал конструкцию за то же время и до той же температуры, что и тепловой поток в условиях обтекания конструкции струей горячих газов, правые части выражений (15) и (16) должны быть равны:

(17)

Рассмотрим полученное выражение. В нем содержатся члены, в которые входит неизвестная функция T4 и неизвестный коэффициент A. Решение уравнения теплопроводности с учетом теплообмена излучением по закону 4-й степени является сложным частным случаем [19]. Не будем использовать его для инженерных расчетов, тем более что поставленная задача может быть решена и без этого.

Видно, что члены с неизвестными функциями сокращаются, так как при них находится одинаковый коэффициент h. Такая ситуация означает, что в случае прогрева эквивалентным тепловым потоком и в случае совместного воздействия на стену теплового и конвективного потоков коэффициент теплоотдачи одинаков. Это вполне допустимое предположение. При пожарах средний коэффициент теплоотдачи от среды к конструкциям (или наоборот) может быть определен, но часто лежит в интервале 12–35 [2, 20, 21]. С учетом изложенного, после сокращения одинаковых членов и коэффициентов получаем:

(18), (19), (20)

Начальная температура среды Tэкв0 равна начальной температуре стенки Tн, поэтому окончательно запишем:

(21)

Получено простое и наглядное выражение, которое легко может быть использовано в инженерных расчетах. Величина приведенного коэффициента облучения ε может быть определена как в работе [13].

Другим способом нахождения теплового потока в ограждающую конструкцию является решение дифференциального уравнения (1), а это может быть сделано только численно с использованием высокого разрешения расчетной области.

Далее приведем решение уравнения без учета лучистого теплообмена между горячим воздухом и стенкой. В этом случае лучистый тепловой поток от нагретых газов учитывается увеличением коэффициента теплоотдачи ά [2]. Продифференцируем уравнение (9):

(22)

Граничные условия без учета лучистого теплообмена со струей горячих газов:

(23)

Граничное условие записано для поверхности, где х = 0.

С учетом этого подставим в выражение граничного условия (23) выражения (9) и (13) при х = 0:

(24)

Преобразуем далее, умножив левую и правую части на -1 и оставляя члены с А в левой части:

(25), (26)

Подставляя в (9), получили решение:

(27), (28)

Путем обратного преобразования Лапласа [6] с помощью таблицы преобразования получаем решение:

(29)

Для решения нашей задачи требуется знать только температуру поверхности тела (стены), поэтому приравняем х = 0:

(30), (31)

Этой формулой можно воспользоваться для получения наглядного представления о ходе графика температуры поверхности при воздействии радиационного теплового потока от пламени и конвективного от нагретой струи газов. Можно скачать файл для программы SmathStudio (бесплатный математический пакет) [22], где автоматизирована постройка графика по (29) при различных исходных параметрах.

Полученное выражение (21) позволяет значительно оптимизировать расчетное обоснование противопожарного расстояния менее 6 м с учетом всех требований Методики и при использовании доступных вычислительных ресурсов.

Таким образом, алгоритм обоснования противопожарного расстояния менее 6 м с учетом полученного выражения следующий:

Определить геометрические размеры поверхности пламени снаружи здания (методика СП 4.13130.2013, полевая модель [6, 10]).
Определить падающий тепловой поток F от поверхности пламени на стену соседнего здания (полевая модель, аналитические методы).
Определить параметры конвективной колонки пожара снаружи здания, в частности температуру в конвективной колонке в местах обтекания стены соседнего здания T0 (полевая модель, модель конвективной колонки в зонной модели CFAST [23]).
Провести расчет по формуле (21)
Сопоставить полученное значение с критическим тепловым потоком для материала стены здания и сделать вывод о допустимости выбранного противопожарного расстояния.

Выводы

В работе рассмотрены возможные пути решения задачи обоснования противопожарного расстояния между зданиями, расположенными в непосредственной близости одно от другого. Дан краткий обзор возможностей моделирующих программ, сделан вывод о необходимости решения поставленной задачи как с использованием численных методов, так и путем решения дифференциального уравнения теплопроводности. Предложен подход к решению задачи по оценке минимальных расстояний между зданиями для случаев, когда необходим учет воздействия конвективного теплопереноса на конструкции здания. Например, в соответствии с п. А.1.1. СП 4.13130.2013 учет воздействия конвективного теплопереноса на конструкции здания следует учитывать при размещении зданий I–IV степеней огнестойкости класса С0 на расстоянии менее 6 м, прочих степеней огнестойкости и классов конструктивной пожарной опасности – на расстоянии менее 10 м.

Обоснование уменьшения противопожарного расстояния менее 6 метров (отступление от Приложения А СП 4.13130)

Похожие записи

Комментарии (0)